一. MD5简介
MD5消息摘要算法(MD5 Message-Digest-Algorithm),是一种被广泛使用的密码散列函数,可以产生出一个128位(16字节)的散列值(hash value),用于确保信息传输完整一致。其典型应用就是对一段信息产生信息摘要,以防止被篡改。 MD5算法以任意长度的信息作为输入进行计算,产生一个128bits的报文摘要,而两个不同的信息所产生的报文摘要是不相同的。因此,MD5常被用于进行数字签名、消息的完整性检测、消息源认证、操作系统的登录认证上等。
二. MD5算法原理
对MD5算法简要的叙述可以为:MD5以512位分组来处理输入的信息,且每一分组又被划分为16个32位子分组,经过了一系列的处理后,算法的输出由四个32位分组组成,将这四个32位分组级联后将生成一个128位散列值。
具体的算法过程如下:
1.填充
在MD5算法中,首先需要对信息进行填充,使其位长对512求余的结果等于448,并且填充必须进行,即使其位长对512求余的结果等于448。填充方法为在信息的后面填充一个1和无数个0,直到满足条件满足。经以上处理,信息的位长(Bits Length)将被扩展至N*512+448,N为一个非负整数,N可以是零。
2.添加原始信息长度
在结果后面附加一个以64位二进制表示填充前信息的长度(单位为bit),如果二进制表示的填充前信息长度超过64位,则取低64位。
经以上处理,信息的位长=N*512+448+64=(N+1)*512,即长度恰好是512的整数倍。这样做的原因是为满足后面处理中对信息长度的要求。
3.初始化变量
信息已被分为512bits一组,每次运算都由前一轮的128位结果和第i块的512bits的值进行运算。初始的128位值为初试链接变量,这些参数用于第一轮的运算,以大端字节序来表示,他们分别为:
A=0x01234567,B=0x89ABCDEF,C=0xFEDCBA98,D=0x76543210。
(每一个变量给出的数值是高字节存于内存低地址,低字节存于内存高地址,即大端字节序。在程序中变量A、B、C、D的值分别为0x67452301,0xEFCDAB89,0x98BADCFE,0x10325476)
4.处理分组数据
每一分组的算法流程如下: 第一分组需要将上面四个链接变量复制到另外四个变量中:A到a,B到b,C到c,D到d。从第二分组开始的变量为上一分组的运算结果,即A = a, B = b, C = c, D = d。 主循环有四轮(MD4只有三轮),每轮循环都很相似。第一轮进行16次操作。每次操作对a、b、c和d中的其中三个作一次非线性函数运算,然后将所得结果加上第四个变量,文本的一个子分组和一个常数。再将所得结果向左环移一个不定的数,并加上a、b、c或d中之一。最后用该结果取代a、b、c或d中之一。 以下是每次操作中用到的四个非线性函数(每轮一个)。
F( X ,Y ,Z ) = ( X & Y ) | ( (~X) & Z )
G( X ,Y ,Z ) = ( X & Z ) | ( Y & (~Z) )
H( X ,Y ,Z ) =X ^ Y ^ Z
I( X ,Y ,Z ) =Y ^ ( X | (~Z) )
(&是与(And),|是或(Or),~是非(Not),^是异或(Xor))
这四个函数的说明:如果X、Y和Z的对应位是独立和均匀的,那么结果的每一位也应是独立和均匀的。 F是一个逐位运算的函数。即,如果X,那么Y,否则Z。函数H是逐位奇偶操作符。 假设Mj表示消息的第j个子分组(从0到15),常数ti是4294967296*abs((sin(i) )的整数部分,i 取值从1到64,单位是弧度(4294967296=232) 现定义:
FF(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + F(b,c,d) + Mj + ti) << s)
GG(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + G(b,c,d) + Mj + ti) << s)
HH(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + H(b,c,d) + Mj + ti) << s)
II(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + I(b,c,d) + Mj + ti) << s)
注意:“<<”表示循环左移位,不是左移位。
这四轮(共64步)是:
第一轮
FF(a ,b ,c ,d ,M0 ,7 ,0xd76aa478 )
FF(d ,a ,b ,c ,M1 ,12 ,0xe8c7b756 )
FF(c ,d ,a ,b ,M2 ,17 ,0x242070db )
FF(b ,c ,d ,a ,M3 ,22 ,0xc1bdceee )
FF(a ,b ,c ,d ,M4 ,7 ,0xf57c0faf )
FF(d ,a ,b ,c ,M5 ,12 ,0x4787c62a )
FF(c ,d ,a ,b ,M6 ,17 ,0xa8304613 )
FF(b ,c ,d ,a ,M7 ,22 ,0xfd469501)
FF(a ,b ,c ,d ,M8 ,7 ,0x698098d8 )
FF(d ,a ,b ,c ,M9 ,12 ,0x8b44f7af )
FF(c ,d ,a ,b ,M10 ,17 ,0xffff5bb1 )
FF(b ,c ,d ,a ,M11 ,22 ,0x895cd7be )
FF(a ,b ,c ,d ,M12 ,7 ,0x6b901122 )
FF(d ,a ,b ,c ,M13 ,12 ,0xfd987193 )
FF(c ,d ,a ,b ,M14 ,17 ,0xa679438e )
FF(b ,c ,d ,a ,M15 ,22 ,0x49b40821 )
第二轮
GG(a ,b ,c ,d ,M1 ,5 ,0xf61e2562 )
GG(d ,a ,b ,c ,M6 ,9 ,0xc040b340 )
GG(c ,d ,a ,b ,M11 ,14 ,0x265e5a51 )
GG(b ,c ,d ,a ,M0 ,20 ,0xe9b6c7aa )
GG(a ,b ,c ,d ,M5 ,5 ,0xd62f105d )
GG(d ,a ,b ,c ,M10 ,9 ,0x02441453 )
GG(c ,d ,a ,b ,M15 ,14 ,0xd8a1e681 )
GG(b ,c ,d ,a ,M4 ,20 ,0xe7d3fbc8 )
GG(a ,b ,c ,d ,M9 ,5 ,0x21e1cde6 )
GG(d ,a ,b ,c ,M14 ,9 ,0xc33707d6 )
GG(c ,d ,a ,b ,M3 ,14 ,0xf4d50d87 )
GG(b ,c ,d ,a ,M8 ,20 ,0x455a14ed )
GG(a ,b ,c ,d ,M13 ,5 ,0xa9e3e905 )
GG(d ,a ,b ,c ,M2 ,9 ,0xfcefa3f8 )
GG(c ,d ,a ,b ,M7 ,14 ,0x676f02d9 )
GG(b ,c ,d ,a ,M12 ,20 ,0x8d2a4c8a )
第三轮
HH(a ,b ,c ,d ,M5 ,4 ,0xfffa3942 )
HH(d ,a ,b ,c ,M8 ,11 ,0x8771f681 )
HH(c ,d ,a ,b ,M11 ,16 ,0x6d9d6122 )
HH(b ,c ,d ,a ,M14 ,23 ,0xfde5380c )
HH(a ,b ,c ,d ,M1 ,4 ,0xa4beea44 )
HH(d ,a ,b ,c ,M4 ,11 ,0x4bdecfa9 )
HH(c ,d ,a ,b ,M7 ,16 ,0xf6bb4b60 )
HH(b ,c ,d ,a ,M10 ,23 ,0xbebfbc70 )
HH(a ,b ,c ,d ,M13 ,4 ,0x289b7ec6 )
HH(d ,a ,b ,c ,M0 ,11 ,0xeaa127fa )
HH(c ,d ,a ,b ,M3 ,16 ,0xd4ef3085 )
HH(b ,c ,d ,a ,M6 ,23 ,0x04881d05 )
HH(a ,b ,c ,d ,M9 ,4 ,0xd9d4d039 )
HH(d ,a ,b ,c ,M12 ,11 ,0xe6db99e5 )
HH(c ,d ,a ,b ,M15 ,16 ,0x1fa27cf8 )
HH(b ,c ,d ,a ,M2 ,23 ,0xc4ac5665 )
第四轮
II(a ,b ,c ,d ,M0 ,6 ,0xf4292244 )
II(d ,a ,b ,c ,M7 ,10 ,0x432aff97 )
II(c ,d ,a ,b ,M14 ,15 ,0xab9423a7 )
II(b ,c ,d ,a ,M5 ,21 ,0xfc93a039 )
II(a ,b ,c ,d ,M12 ,6 ,0x655b59c3 )
II(d ,a ,b ,c ,M3 ,10 ,0x8f0ccc92 )
II(c ,d ,a ,b ,M10 ,15 ,0xffeff47d )
II(b ,c ,d ,a ,M1 ,21 ,0x85845dd1 )
II(a ,b ,c ,d ,M8 ,6 ,0x6fa87e4f )
II(d ,a ,b ,c ,M15 ,10 ,0xfe2ce6e0 )
II(c ,d ,a ,b ,M6 ,15 ,0xa3014314 )
II(b ,c ,d ,a ,M13 ,21 ,0x4e0811a1 )
II(a ,b ,c ,d ,M4 ,6 ,0xf7537e82 )
II(d ,a ,b ,c ,M11 ,10 ,0xbd3af235 )
II(c ,d ,a ,b ,M2 ,15 ,0x2ad7d2bb )
II(b ,c ,d ,a ,M9 ,21 ,0xeb86d391 )
所有这些完成之后,将a、b、c、d分别在原来基础上再加上A、B、C、D。 即a = a + A,b = b + B,c = c + C,d = d + D 然后用下一分组数据继续运行以上算法。
5.输出
最后的输出是a、b、c和d的级联。(a+b+c+d)
三、实现代码(需要message.txt明文文件)
#include<iostream>
#include<string>
#include<memory.h>
#include <fstream>
using namespace std;
// 定义 F G H I
#define shift(x, n) (((x) << (n)) | ((x) >> (32 - (n)))) // 右移的时候,高位要补0,而不是补充符号位
#define F(x, y, z) (((x) & (y)) | ((~x) & (z)))
#define G(x, y, z) (((x) & (z)) | ((y) & (~z)))
#define H(x, y, z) ((x) ^ (y) ^ (z))
#define I(x, y, z) ((y) ^ ((x) | (~z)))
char sstr[500];
string convertToHex(int num) {
const char str16[] = "0123456789abcdef";
int hexNum;
string temp = "";
string hexString = "";
for (int i = 0; i < 4; i++) {
// 一个小块32bit,每次处理一个字节,所以循环4次
temp = "";
/*
* 1 << 8 = 2^8 = 256,对256取模,即取32bit的低8位
* &0xff 即把 除低8位外的所有位都置0,得低8位的值
* 逆序处理每个字节,因存储方式和显示方式相反(大小端关系)
*/
hexNum = ((num >> i * 8) % (1 << 8)) & 0xff;
/*
* 因为max(hexNum) 255,故转换为hex只需要两次循环即可
* tmp.insert(0, 1, str16[hexNum % 16]) 意为 在tmp的第0个位置插入一个str[hexNum%16]
*/
for (int j = 0; j < 2; j++) {
temp.insert(0, 1, str16[hexNum % 16]);
hexNum = hexNum / 16;
}
hexString += temp;
}
return hexString;
}
string getMD5(string str) {
// 一种移位的方法,参考自 百度百科(MD5)
const unsigned s[64] = {
7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22,
5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20,
4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23,
6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21
};
// ti 是 4294967296*abs(sin(i))的整数部分(1≤i≤64, 2^32=4294967296)
const unsigned k[64] = {
0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee,
0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be,
0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa,
0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed,
0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c,
0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05,
0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039,
0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1,
0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391
};
// 初始化变量 链接变量
unsigned int A = 0x67452301;
unsigned int B = 0xefcdab89;
unsigned int C = 0x98badcfe;
unsigned int D = 0x10325476;
int strLength = str.length();
/*
* 填充:遵循 bit lengths = 448 (mod 512)
* 在原始str后,填充一个1和无数个0,直至满足上面一个条件
* +8 是因为最后的64bit是用于放置str长度信息
* +1 是因为至少有一个大块存放512bits
*/
unsigned int blockNum = ((strLength + 8) / 64) + 1; // 计算需要多少个大块
/*
* 填充后的字符串长度为512bits,分为16个小块,每小块32bits
*/
unsigned int *strByte = new unsigned int[blockNum * 16];
memset(strByte, 0, sizeof(strByte) * blockNum * 16);
for (unsigned int i = 0; i < strLength; i++) {
/*
* 传入的str,其中str[i]表示一个char = 8 bits
* 而strByte[i]的大小为32bits
* 故对于传入字符串的处理str的前4个char都放进同一个小块当中
* 0>>2 1>>2 2>>2 3>>2 结果都为0,即前4位都存储在strByte[0]当中
* << ((i%4)*8) 是实现从低到高进行存储
*/
strByte[i >> 2] |= (str[i]) << ((i % 4) * 8);
}
/*
* 填充规则:在str后,填充一个1和无数个0,即添加一个0x80 -> 10000000
* strLength >> 2是计算str可以占多少个小块,则0x80就跟在最后一个char的后面
* (strLength % 4 * 8) 计算0x80应该存在于每个小块的哪个位置
* [][][0x80][str.end()] 大端方式
*/
strByte[strLength >> 2] |= 0x80 << ((strLength % 4) * 8);
/*
* 低64位 存储 信息填充前 信息的长度
* str 一个char = 8 bits,故 str.length()*8 即总长度*/
strByte[blockNum * 16 - 2] = strLength * 8;
/*
* 对每一个的32bits的小块进行处理
* FF(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + F(b,c,d) + Mj + ti) << s)
* GG(a ,b ,c ,d ,Mj ,s ,ti ) 操作为 a = b + ( (a + G(b,c,d) + Mj + ti) << s)
* HH(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + H(b,c,d) + Mj + ti) << s)
* II(a ,b ,c ,d ,Mj ,s ,ti) 操作为 a = b + ( (a + I(b,c,d) + Mj + ti) << s)
* 每轮有16次的操作 每次操作对a b c 和 d 中其中三个作一次非线性函数运算
* 将结果加上第四个变量,文本的一个子分组 Mj和一个常数 ti(即k[i])
*/
for (unsigned int i = 0; i < blockNum; i++) {
unsigned int a = A;
unsigned int b = B;
unsigned int c = C;
unsigned int d = D;
unsigned int f, g; // g for choose the Mj
for (unsigned int j = 0; j < 64; j++) {
if (j < 16) {
f = F(b, c, d);
g = j;
} else if (j < 32) {
f = G(b, c, d);
g = (5 * j + 1) % 16;
} else if (j < 48) {
f = H(b, c, d);
g = (3 * j + 5) % 16;
} else {
f = I(b, c, d);
g = (7 * j) % 16;
}
unsigned tmpD = d;
d = c;
c = b;
b = b + shift((a + f + k[j] + strByte[i * 16 + g]), s[j]);
a = tmpD;
}
A = a + A;
B = b + B;
C = c + C;
D = d + D;
}
// 将结果进行级联
return convertToHex(A) + convertToHex(B) + convertToHex(C) + convertToHex(D);
}
void recursiveInput() {
cout << "请输入数字选择读取明文模式:\n 1.手动输入明文\n 2.读取明文messgae.txt文件"<<endl;
int i;
cin >> i;
cout <<endl;
if(i == 1) {
cout << "input the plaintext: ";
string ss;
cin >> ss;
string s = getMD5(ss);
cout << "There is your MD5 encryption result: " + s << endl;
char filename[] = "result.txt";
ofstream fout(filename);
fout << "The MD5 encryption result is : " << s <<endl;
fout.close();
}
else if(i == 2) {
ifstream fin("messgae.txt");
if(!fin) {
cout << "Error!!! There is no file named message." << endl;
}
else {
fin.getline(sstr, 400);
fin.close();
string s = getMD5(sstr);
cout << "input plaintext: ";
cout<<sstr << endl;
cout << "There is your MD5 encryption result: " + s << endl;
char filename[] = "result.txt";
ofstream fout(filename);
fout << "The MD5 encryption result is : " << s <<endl;
fout.close();
}
}
else {
cout << "输入错误!"<<endl;
}
}
int main() {
recursiveInput();
return 0;
}
四、实现效果
1.首先是运行的初始界面,可以选择两种方式之一进行信息加密,1 是手动输入明文进 行加密,2 是读取 message.txt 中的明文。
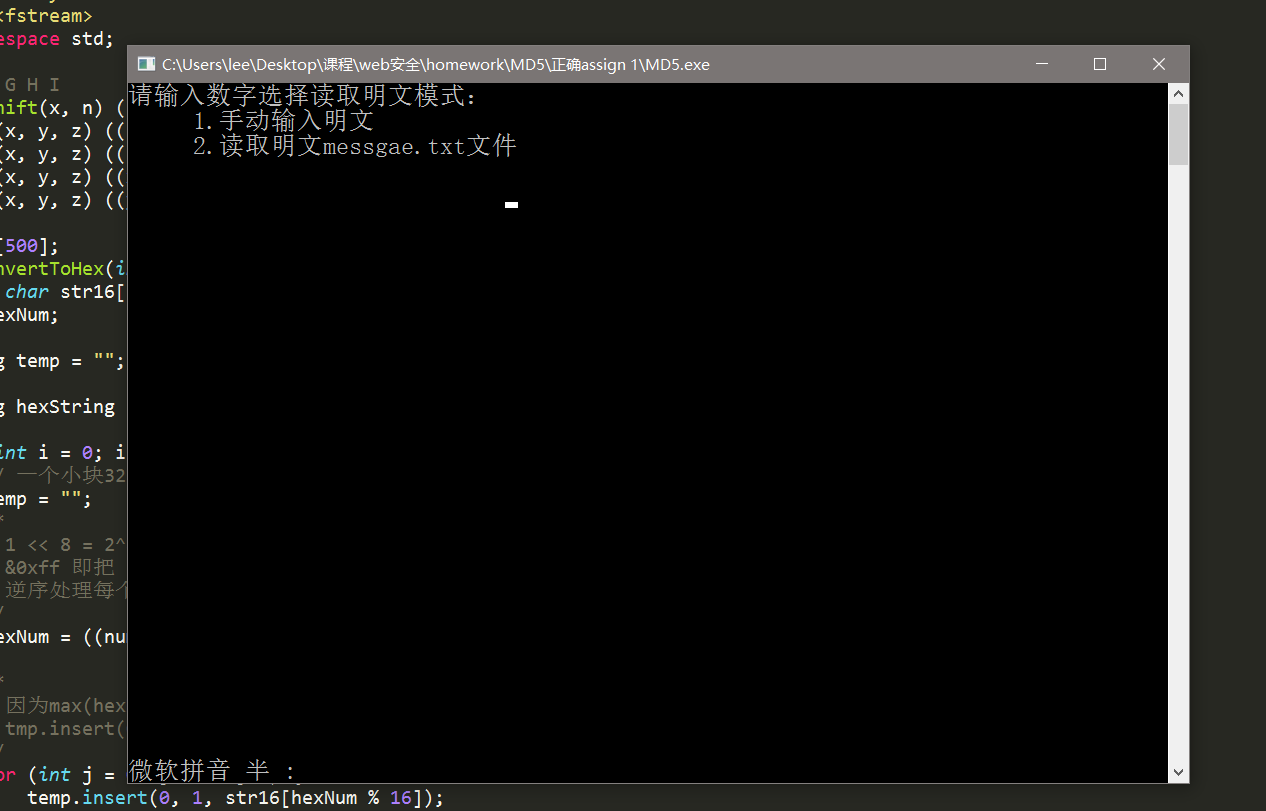
2.手动输入明文进行加密效果。加密结果会输出到 result.txt 文件中。
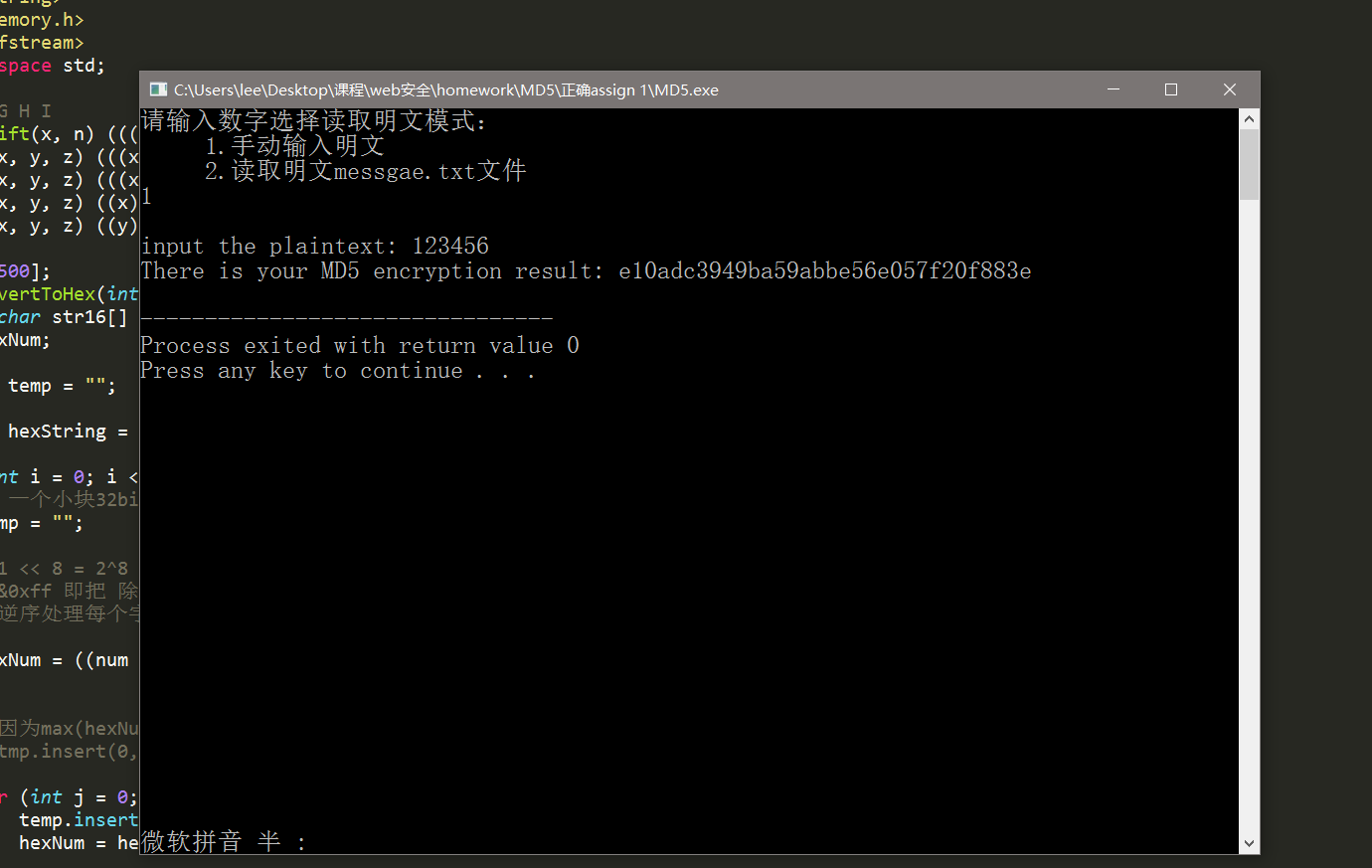
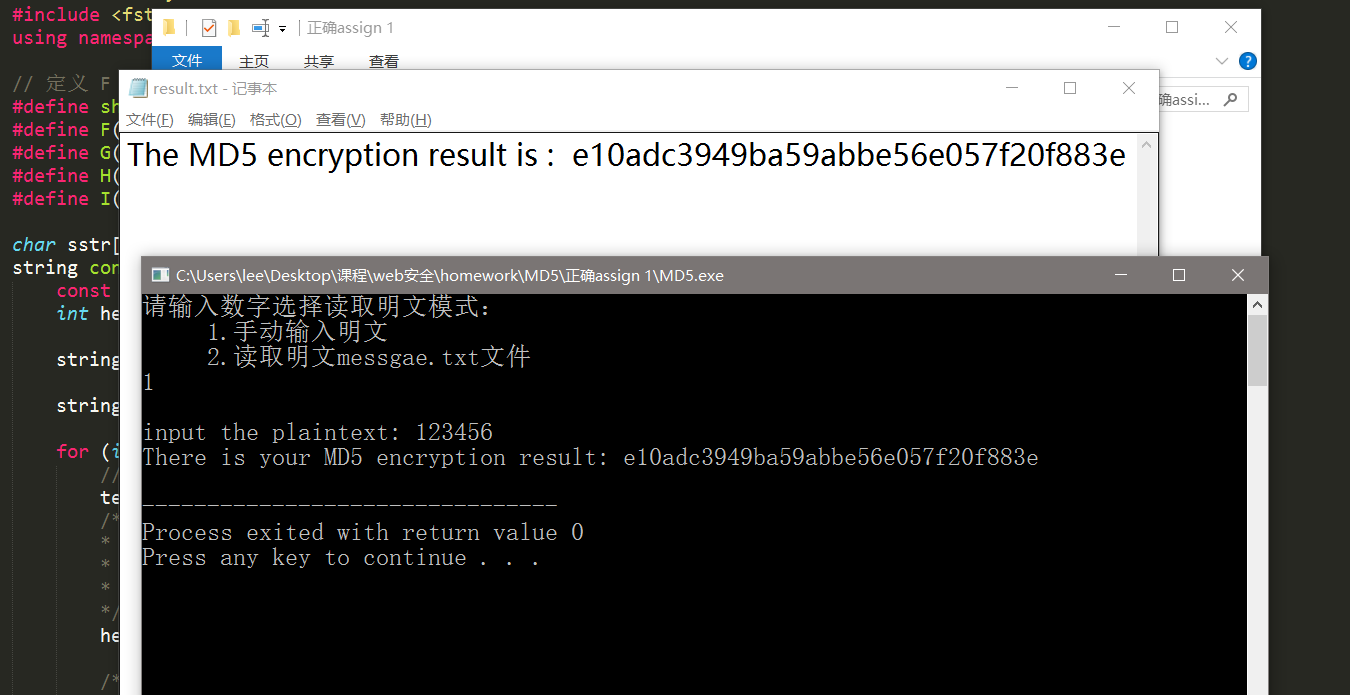
3.读取 message.txt 中的明文进行加密并将结果输出到 result.txt 中。
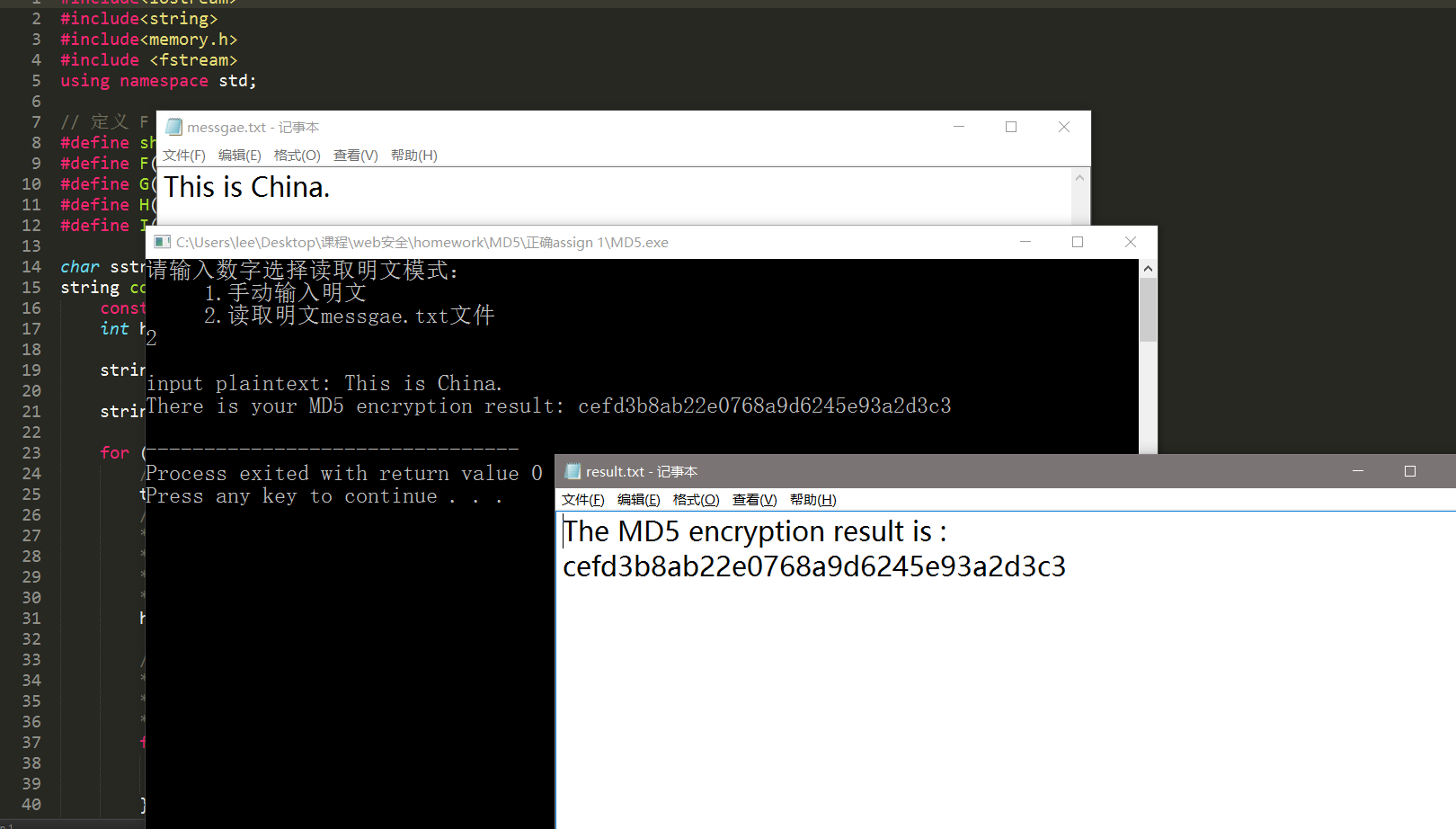
4.这是加密结果与在线加密标准结果的对比,加密结果正确。
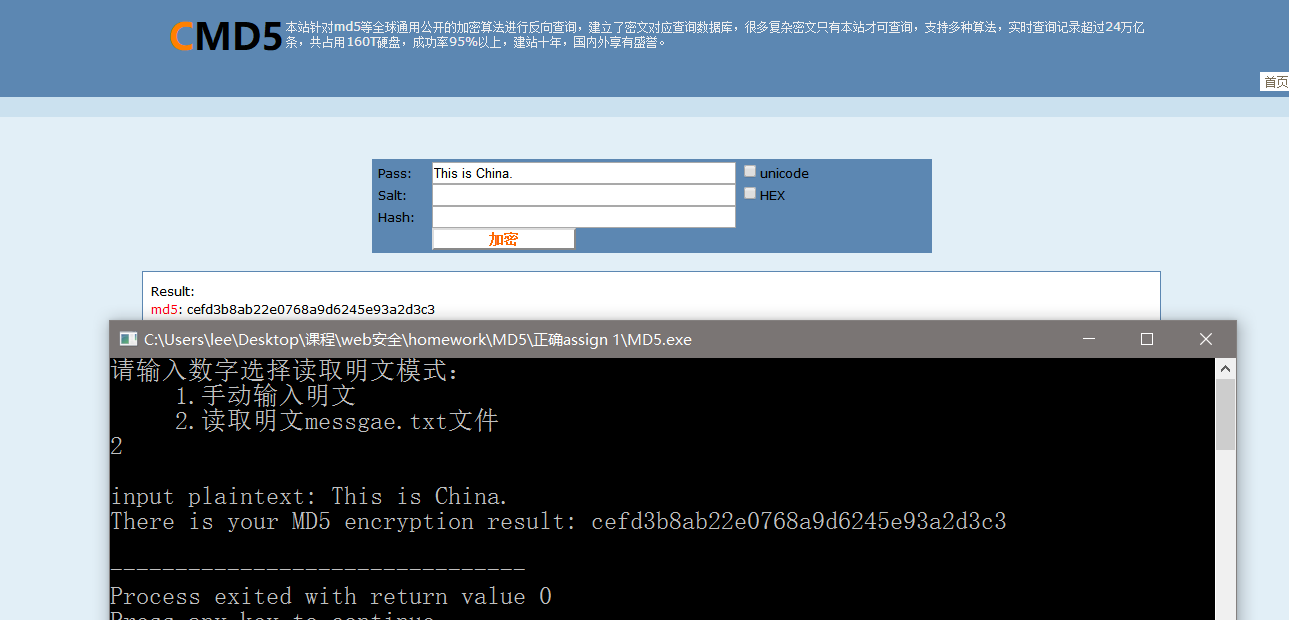
作为一个安全的摘要算法在设计时必须满足两个要求——其一是寻找两个输入得到相 同的输出值在计算上是不可行的,这就是我们通常所说的抗碰撞的;其二是找一个输出,能 得到给定的输入在计算上是不可行的,即不可从结果推导出它的初始状态——MD5 已经无法满足第一个条件,也就是说 MD5 已经不安全了。但是碰撞概率很低,而且也没有特别高效的找出碰撞的算法,所以对其的破解,据网上搜索的结果,主流的都不是针对算法本身,而是针对算法的使用方式。比如,对未经加密的一个密码库运用 MD5 产生对应的 MD5 密码库 a,然后如果能够查询到网站服务器上的经过 MD5 处理的密码库数据 b,那么就可以用 b 和 a 中数据直接进行匹对,找到 a 中对应 MD5 密码后,对应回其原密码就好了。其关键在于首先 a 要足够的大,可能包含到所需的密码,第二是要得到 b 中的数据.网络上有 一些 MD5 查询破解网站,其就是有这样的一个密码库 a,提交一串 MD5 后,如果其数据库中刚好也有这个数据,即可破解成功。

